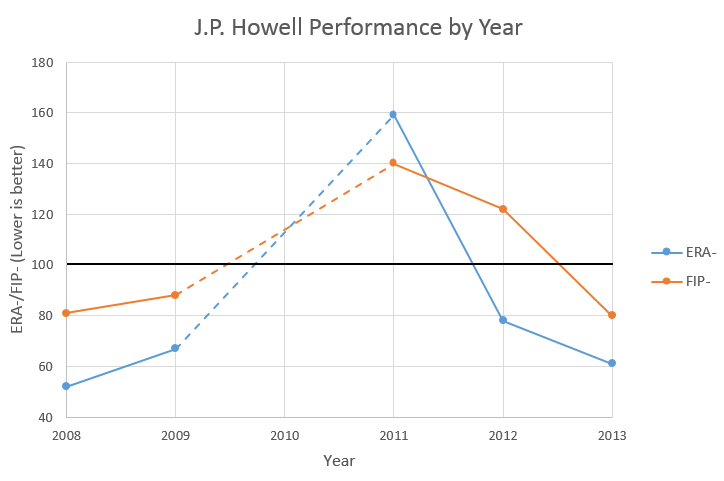
Projecting the performance of the Dodgers’ 2014 starting outfield is a difficult task. If the season started today, the Dodgers would have four major league quality outfielders fighting for three spots. Trade rumors are still swirling around Matt Kemp and Andre Ethier in particular, so there’s a strong possibility that these numbers will change significantly before opening day. The Dodgers had the same theoretical problem last year, but it didn’t really impact playing time, since outfielder was almost always injured.
There’s also Joc Pederson and Scott Van Slyke, but they’ll be covered in a separate piece on bench/minor league contributors after those portions of the rosters get more set.
The format remains the same as the last Steamer projections post. First, I’ll show a comparison between the player’s 2013 statistics and their 2014 Steamer projection. I’ll then describe the specifics of the projection, then I’ll predict if the player will finish over or under the projected WAR total and explain the rationale behind my prediction.
I’m adding my own predictions because these projection systems can be flawed or based on different assumptions than what I have. It might be fun to revisit the accuracy of these predictions against the projections after the season is over. As we all know, predicting baseball is very difficult, so I don’t have much confidence in my predictions over the projections.
Matt Kemp
|
Season
|
PA
|
HR
|
SB
|
BB%
|
K%
|
ISO
|
BABIP
|
AVG
|
OBP
|
SLG
|
wOBA
|
wRC+
|
BsR
|
Off
|
Def
|
WAR
|
|
2013
|
290
|
6
|
9
|
7.6 %
|
26.2 %
|
.125
|
.353
|
.270
|
.328
|
.395
|
.316
|
103
|
1.7
|
2.7
|
-15.3
|
-0.4
|
|
2014
|
567
|
22
|
13
|
9.2 %
|
24.3 %
|
.192
|
.329
|
.271
|
.342
|
.464
|
.346
|
125
|
0.4
|
16.1
|
-6.4
|
2.9
|
Projection Synopsis: Steamer projects a huge rebound for Kemp, expecting him to maintain consistent playing time while producing better power and walk numbers than his disastrous 2013 campaign. Even with this rebound, the numbers here most closely resemble his full 2012 season and not the better numbers that he produced before.
Over/Under prediction: Sigh. I want to be wrong so badly, but I have to take the under. I have serious doubts about his ability to stay healthy for a full season, and I think his speed numbers and defensive value will be lower than what is projected here due to the ankle and hamstring injuries that he suffered last season. Like I said, I badly hope that I’m wrong, because Kemp is so amazing to watch when he’s healthy.
Andre Ethier
|
Season
|
PA
|
HR
|
SB
|
BB%
|
K%
|
ISO
|
BABIP
|
AVG
|
OBP
|
SLG
|
wOBA
|
wRC+
|
BsR
|
Off
|
Def
|
WAR
|
|
2013
|
553
|
12
|
4
|
11.0 %
|
17.2 %
|
.151
|
.315
|
.272
|
.360
|
.423
|
.340
|
120
|
0.5
|
13.2
|
-2.7
|
2.9
|
|
2014
|
444
|
12
|
3
|
9.9 %
|
18.3 %
|
.162
|
.310
|
.269
|
.348
|
.431
|
.338
|
119
|
-0.7
|
8.7
|
-1.1
|
2.3
|
Projection synopsis: Steamer projects that Ethier will be the outfielder who loses the most playing time due to the outfielder surplus. That’s probably true, if everybody remains healthy. It predicts a slight increase in power and a slight reduction in walk rate, resulting in wRC+ and wOBA values very similar to what he managed last season.
Over/under prediction: Over, for several reasons. I think the playing time estimates for both Kemp and Crawford are high (given higher likelihoods of injury), which hurts Ethier’s projected value. If Ethier’s playing time does end up being this low, I think his offensive numbers will be higher since he’ll be facing fewer lefties. The defensive value being projected here is probably a bit higher than what I’d expect, because I’m a bit skeptical of how the advanced defensive metrics graded him last season. But the reduction in defensive value can potentially be offset by an improved offensive performance. That is, unless he’s traded.
Carl Crawford
|
Season
|
PA
|
HR
|
SB
|
BB%
|
K%
|
ISO
|
BABIP
|
AVG
|
OBP
|
SLG
|
wOBA
|
wRC+
|
BsR
|
Off
|
Def
|
WAR
|
|
2013
|
469
|
6
|
15
|
6.0 %
|
14.1 %
|
.124
|
.321
|
.283
|
.329
|
.407
|
.322
|
108
|
5.0
|
9.1
|
4.0
|
2.9
|
|
2014
|
570
|
12
|
18
|
6.3 %
|
15.7 %
|
.140
|
.309
|
.274
|
.324
|
.414
|
.322
|
108
|
2.0
|
7.0
|
-3.4
|
2.2
|
Projection synopsis: Steamer is projecting a reduction in BABIP and an increased strikeout rate, but an increase in power, which results in precisely the same wOBA and wRC+ as he produced last season. Increased playing time, but reduction in defensive value combine to produce a WAR that is about 0.7 lower than 2013.
Over/under prediction: Under. This projection was probably the hardest for me to guess, since I think all of the assumptions are just about right. The increase in power makes sense. Crawford’s career ISO is .147 and the above table don’t include postseason numbers, when Crawford hit four homeruns.
The defensive value drop, which is the biggest change, makes some amount of sense. Defensive metrics were very split on their evaluation of Crawford last season. Crawford had a UZR (ultimate zone rating) of 8.6 runs above average. However, he had a DRS (defensive runs saved) of only 1 run above average. While the UZR is pretty close to Crawford’s career level and DRS is lower, Crawford’s hamstring injury last year may have impacted his performance. Defensive metrics are so fickle that it’s hard to tell what’s right and what’s not.
I ended up taking the under (after a lot of deliberation) because I think the PA count is too high. It’s almost a sure bet that Crawford will miss at least some amount of time due to injury next season. But I could have gone either way on this one.
Yasiel Puig
|
Season
|
PA
|
HR
|
SB
|
BB%
|
K%
|
ISO
|
BABIP
|
AVG
|
OBP
|
SLG
|
wOBA
|
wRC+
|
BsR
|
Off
|
Def
|
WAR
|
|
2013
|
432
|
19
|
11
|
8.3 %
|
22.5 %
|
.215
|
.383
|
.319
|
.391
|
.534
|
.398
|
160
|
-4.2
|
25.1
|
-0.7
|
4.0
|
|
2014
|
618
|
26
|
20
|
8.5 %
|
19.9 %
|
.211
|
.330
|
.290
|
.359
|
.502
|
.370
|
141
|
-1.8
|
26.9
|
-3.3
|
4.5
|
Projection Synopsis: Puig’s Steamer projection expects him to maintain the walk rate and power that he displayed over the course of last season, with a slightly reduced strikeout rate. It projects an overall drop in his offensive value, mostly due to a steep drop in BABIP. It expects his defensive value to be slightly lower, but also expects his baserunning value to be slightly higher.
Over/under prediction: Over. Taking the “over” on a 4.5 win projection is bold, but there are a few factors that cause me to think that the projected value is a bit low. The first is the steep decline in BABIP. The likelihood of Puig matching his 2013 BABIP is low, but his skillset still makes a .330 projection a bit too low. Puig seems like the only outfielder who will be playing every day when healthy, so I think the plate appearance count here is potentially low (barring injury, of course). The projected walk rate might also be a bit low, since his overall walk rate increased dramatically throughout the course of last season.
Additionally, I think that the decline in defensive value here is a bit unusual. Puig has looked anywhere between lost and amazing on defense, but I can’t understand why Steamer is projecting a decline. The magnitude of the projected decline is small (2.6 runs), but it’s puzzling.
Put all of that together, and I think Puig is set up for a great sophomore season. Potentially MVP level, even.
Overall
2013 outfield (primary starter) fWAR: 9.4
2014 outfield (primary starter) fWAR: 11.9
Conclusions: Steamer is projecting an increase of about 2.5 wins from the starting outfield group in 2014. This is mainly due to an increase of 3.3 wins from Matt Kemp. If Kemp can rebound with the magnitude that is projected here, it will be a huge boost to the Dodgers’ ability to contend in the 2014 season. While these projections are still fluid (based on a roster that is not yet complete), it is still encouraging that at least one projection system is predicting a rebound of this magnitude.